
Adding flats / Removing sharpsĪ similar logic shows why the second-to-last flat also shows the key.
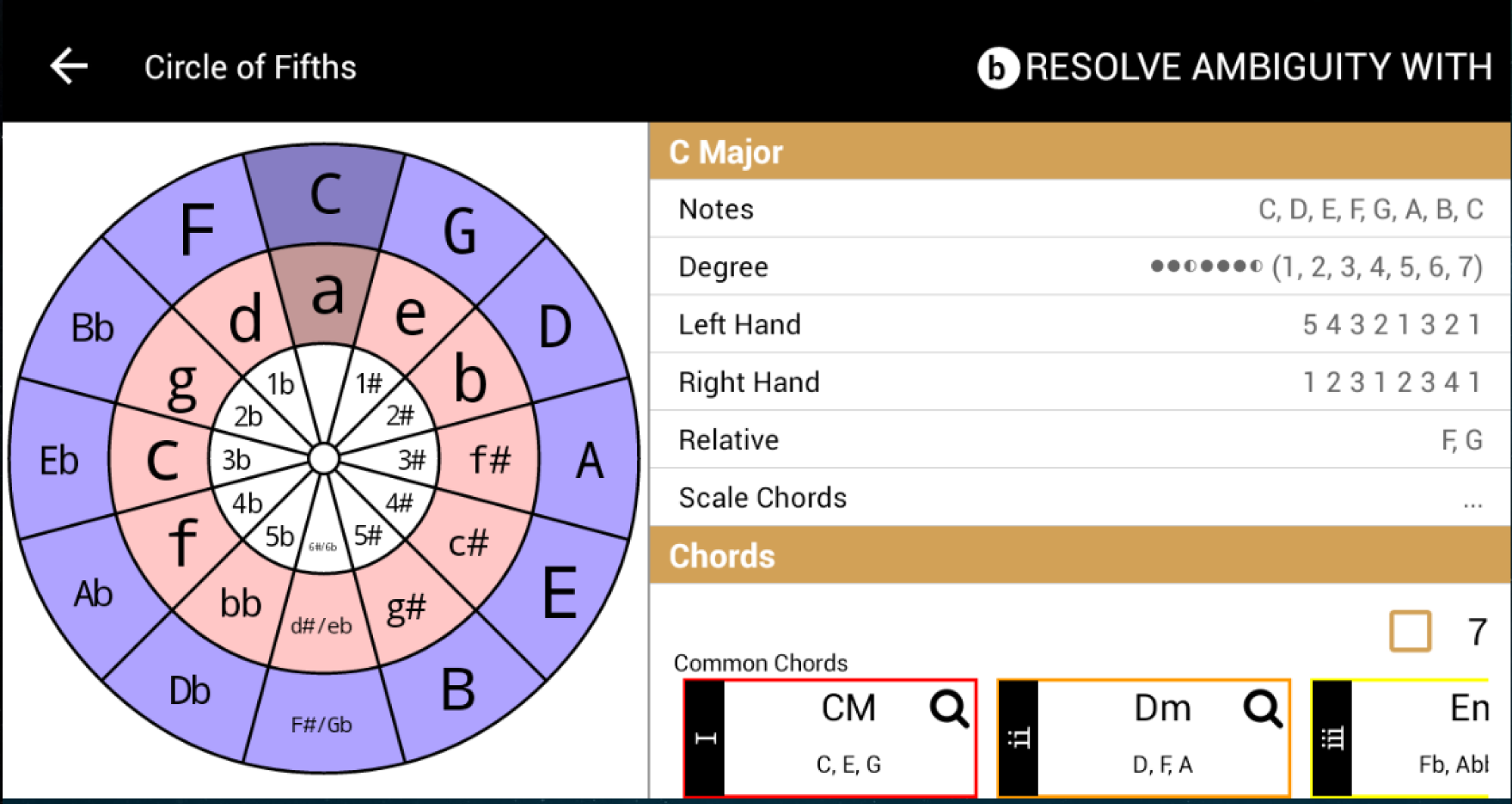
The Bb is then sharped to result in C major. The Eb from Bb major was "sharped" to create the leading tone for F major, leaving only Bb. The next step in the circle of fifths is F major, which has only Bb. Put simply: The sharp introduced as one goes around the circle of fifths is always the leading-tone (i.e., scale degree seven, or, one step before the tonic) of the new scale.Īdding a sharp is "the same" as subtracting a flat, which is why when key signatures switch from sharps to flats, the number of flats in the key signature is reduced until there are none and the circle has returned to C major.Īs a brief example, Bb major has two flats: Bb and Eb.
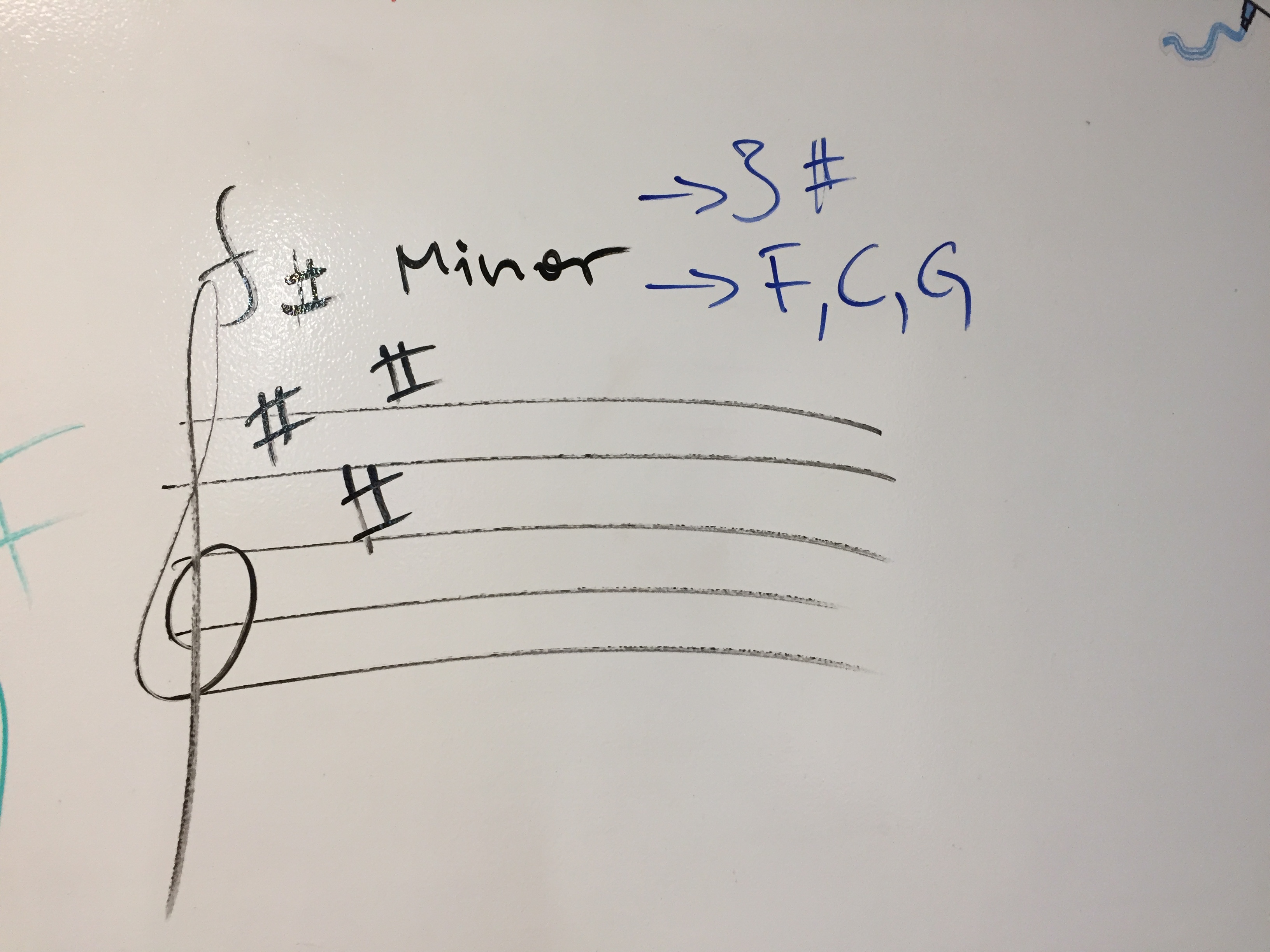
This is achieved by raising scale degree 4 of the original scale a half step. Notice that all the intervals line up except for degrees 3-4-5 or the original scale, which correspond to 6-7-8 of the new scale. "new" scale 1 W 2 W 3 H 4 W 5 W 6 W 7 H 8 Starting scale: 5 W 6 W 7 H 1 W 2 W 3 H 4 W 5 Now we're going to start the "next" major scale beginning on degree 5 of the previous scale. This gives us scale degrees and intervals between as follows: Consider the following definition of a major scale (W = Whole Step H = Half step):


 0 kommentar(er)
0 kommentar(er)
